La proposición que elegí es la siguiente:
- All philosophers are logical;
An illogical man is always obstinate
El primer paso que realicé fue asignarle una expresión a cada proposición, a la característica de ser lógico le asigné la variable x ya que las dos proposiciones giran en torno esta característica:
- x = logical
- F(x) = philosophers
- M(x) = man
- O(x) = obstinate
Teniendo estas expresiones, lo siguiente que realicé fue buscar los cuantificadores de los cuales solo utilicé es el de todos ∀; de tal manera que las expresiones quedan de la siguiente manera:
All philosophers are logical
An illogical man is always obstinate
De las proposiciones anteriores podemos concluir que:
An illogical man is not a philosopher
All philosophers are not obstinate
En comentarios pueden dejar cualquier duda o aclaración,
¡Saludos!


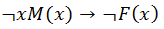

Falta un predicato para lo de hombre lógico y falta un conectivo cuando combinas eso con M(x)... Van 6 pts.
ReplyDelete