Developer: Diagramas de decisión binaria

Primero que nada hay que definir que es un diagrama de decisión. Los diagramas de decisión ayudan a realizar elecciones adecuadas entre distintas posibilidades. Su estructura permite seleccionar todas las diferentes opciones para conocer los diferentes escenarios.

Las ventajas de un árbol de decisión son:

Permite la clasificación de nuevos casos
Facilita la interpretación de la decisión analizada.
Se puede analizar el comportamiento respecto a una determinada decisión.
Número de variables reducido.

Diagramas de Decisión Binaria

Los diagramas de decisión binaria (DDB o BDD en inglés) son estructuras de datos que se utilizan para representar funciones booleanas, también son representaciones de conjuntos y relaciones en los cuales se pueden hacer operaciones.

Un DDB es un grafo acíclico dirigido con raíz que permite representar funciones booleanas. En general estos diagramas tienen nodos de decisión, estos nodos contienen una variable booleana(ya sea un 0 o un 1) y están conectados a dos nodos que son sus hijos. Todos los nodos se encuentran en el mismo nivel y solo aparecen una sola vez en cada rama; y deben de exitir dos nodos que se conocen como terminales y por conveniencia se les llama terminal-0 y terminal-1.

En palabras más claras una diagrama de decisión binaria es un grafo dirigido acícliclo que representa una función booleana como una serie de sentencias if...then...else anidadas. Estos diagramas nos permiten representar los distintos estados de un sistema.

Para simplificar o reducir un DDB se deben aplicar las siguientes dos reglas:

Unir las estrucuturas matemáticas que son iguales
Eliminar los nodos que tengan dos hijos iguales

Las ventajas de utilizar un diagrama reducido son:

Son únicos para una expresión booleana
Sus variables están ordenadas

Tarea 3

Para esta semana la tarea es modelar una proposición utilizando mínimo 3 variables y cuatro conectores, de esta proposición hay que obtener el diagrama de decisión binario y reducirlo.

Como proposición utilicé la siguiente:

(p v q) ^ (¬r ^ q) v (p ^ r)

Esta es la tabla de verdad de la expresión anterior

p	q	r	p v q	¬r ^ q	p ^ r	(p v q) ^ (¬r ^ q)	(p v q) ^ (¬r ^ q) v (p ^ r)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0
0	1	0	1	1	0	1	1
0	1	1	1	0	0	0	0
1	0	0	1	0	0	0	0
1	0	1	1	0	1	0	1
1	1	0	1	1	0	1	1
1	1	1	1	0	1	0	1

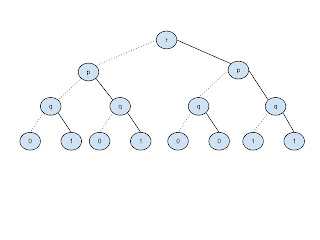
Ahora el diagrama de decisión binario, es el siguiente:

Aplicando las dos reglas que mencioné anteriormente para reducir un diagrama obtenemos lo siguiente:

Diagramas de decisión binario reducido ordenado(DDBRO)

Esta parte también se debe realizar para completar la tarea, un DDBRO consiste darle un diferente orden a las variables de entrada del diagrama original para obtener un diagrama diferente y por consecuencia el diagrama reducido será tambien diferente

Para esta parte utilicé el orden r < q< r , y a continuación les muestro el DDBTO